Metamorphosen ebener Kurven in kleinen Schritten (I)
Formwandel in der Natur geschieht kontinuierlich, die Baumnuss entwickelt sich durch unendlich viele Zwischenstufen zum Nussbaum.
Auch der Formwandel geometrischer Formen lässt sich so auffassen. Ein gleichseitiges Dreieck kann in ein rechtwinkliges verwandelt werden, indem die Spitze des Dreiecks auf einer Parallelen zu Dreiecksbasis verschoben wird. Zwischen rechtwinklig und gleichseitig gibt es unendlich viele Zwischenformen, die weder gleichseitig noch rechtwinklig sind. In einer Zeichnung kann ich immer nur ein paar wenige Zwischenstadien angeben und ob ich deren zwei oder zehn zeichne ist für den Verwandlungsprozess belanglos. Zwischen irgendwelchen zwei Stadien in diesem Prozess liegen stets unendlich viele weitere Stadien. Die kontinuierliche Verwandlung lässt sich höchstens in der Vorstellung nachvollziehen. Dies genügt auch vollauf, denn ich bin mir sicher, dass kein Zwischenstadium etwas wesentlich Neues zeigen würde.
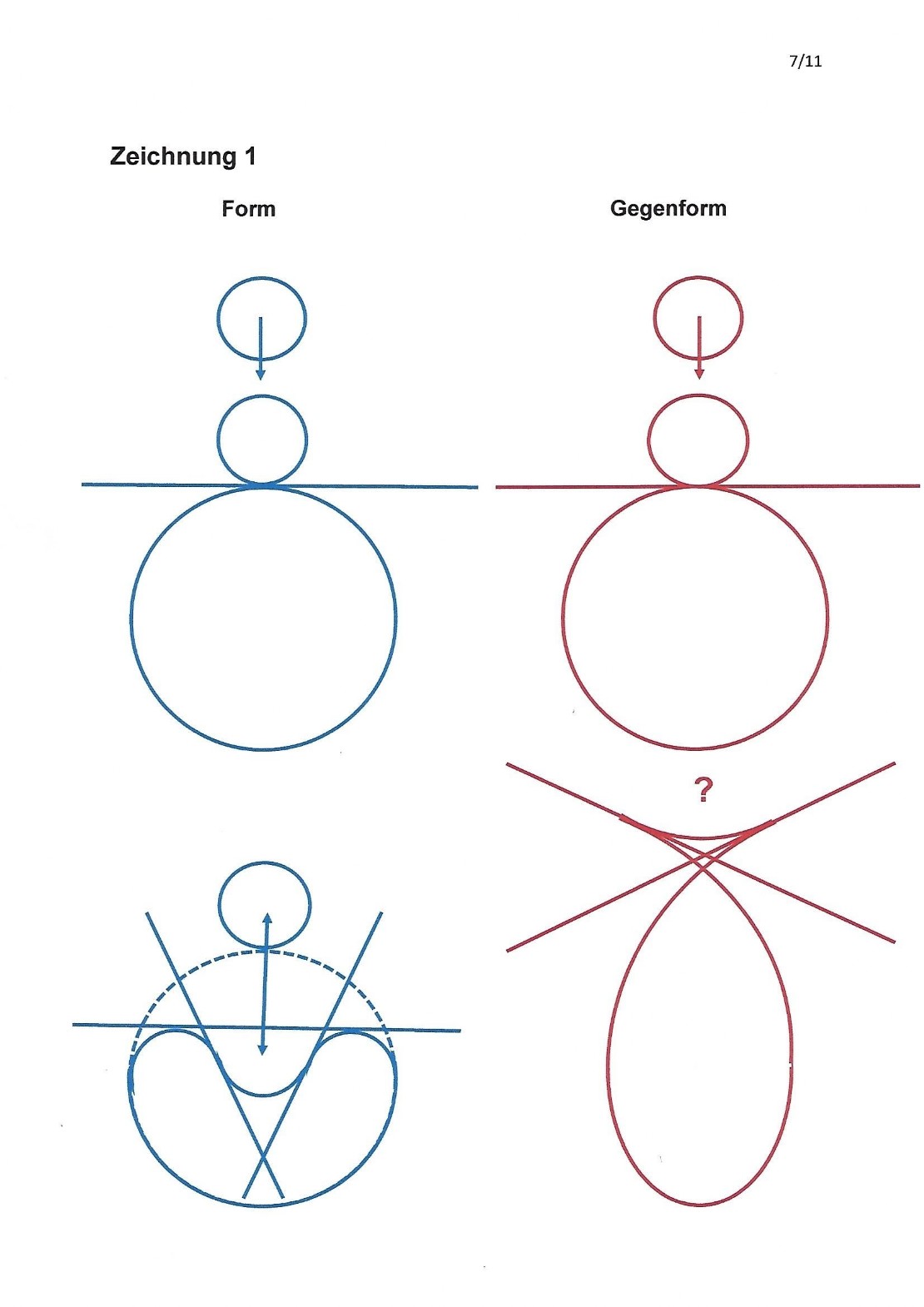
Im Gegensatz dazu gibt es aber Fälle von Metamorphosen, in denen ganz plötzlich sprunghafte Änderungen eintreten, die ich erstaunlich finde. Im Buch von Louis Locher-Ernst „Freie Geometrie ebener Kurven“ (FGEK)*, sind sehr schöne Kurven-Metamorphosen, zum Beispiel auf Seite 73, die Figuren 60a bis 60i, gezeichnet. Die Form und ihre Gegenform in Figur 60a habe ich ausgesucht, um eine derartige sprunghafte Änderung zu zeigen. Die beiden Formen sind in Zeichnung 1 unten zu sehen.
Ich habe mir die Aufgabe gestellt, zuerst die blaue „Dellen-Form“, links unten und dann auch deren rot gezeichnete Gegenform rechts unten aus einem Kreis in ganz kleinen Verwandlungsschritten abzuleiten.
Die blauen Kreise
Zunächst betrachte ich nur die blauen Kreise links in Zeichnung 1. Der grosse Kreis soll ein plastisch verformbarer Ring sein, während der kleine Kreis dagegen eine starre Scheibe sein soll.
Plastisch verformbar heisst: Verformungen an diesem Ring bleiben bestehen, auch wenn die verformende Kraft aufhört einzuwirken.
Der kleine Kreis wird nun gegen den grossen Kreis bewegt.
Die Achter-Form
Als Erstes berühren sich die beiden Kreise, es entsteht eine Achter-Form. Sie hat einen unteren grossen Bauch und einen oberen kleinen Kopf, beide berühren sich in einem Punkt. Die Singularitäten der Achter-Form sind zunächst ein Doppel-Punkt und eine Doppel-Tangente.
Das weitere Vorgehen ist klar: Sobald ich die Bewegung fortsetze, drückt der kleine starre Kreis die gewünschte Delle in den grossen plastisch verformbaren Kreisring und die „Dellen-Form“ mit einer Doppel-Tangente und zwei Wende-Tangenten entsteht (Zeichnung 1 links unten).
*Louis Locher-Ernst / Georg Unger, „Freie Geometrie ebener Kurven“, Verlag am Goetheanum, 2. Überarbeitet Auflage, herausgegeben von Renatus Ziegler und Bettina Kistler, 2016
Singularitäten der Achter-Form
Die Kreise von denen ich ausgehe, weisen keine Singularitäten auf. Sie können als Einfache Bogen bezeichnet werden, deren Enden zusammenfallen und die dort eine gemeinsame Tangente aufweisen.
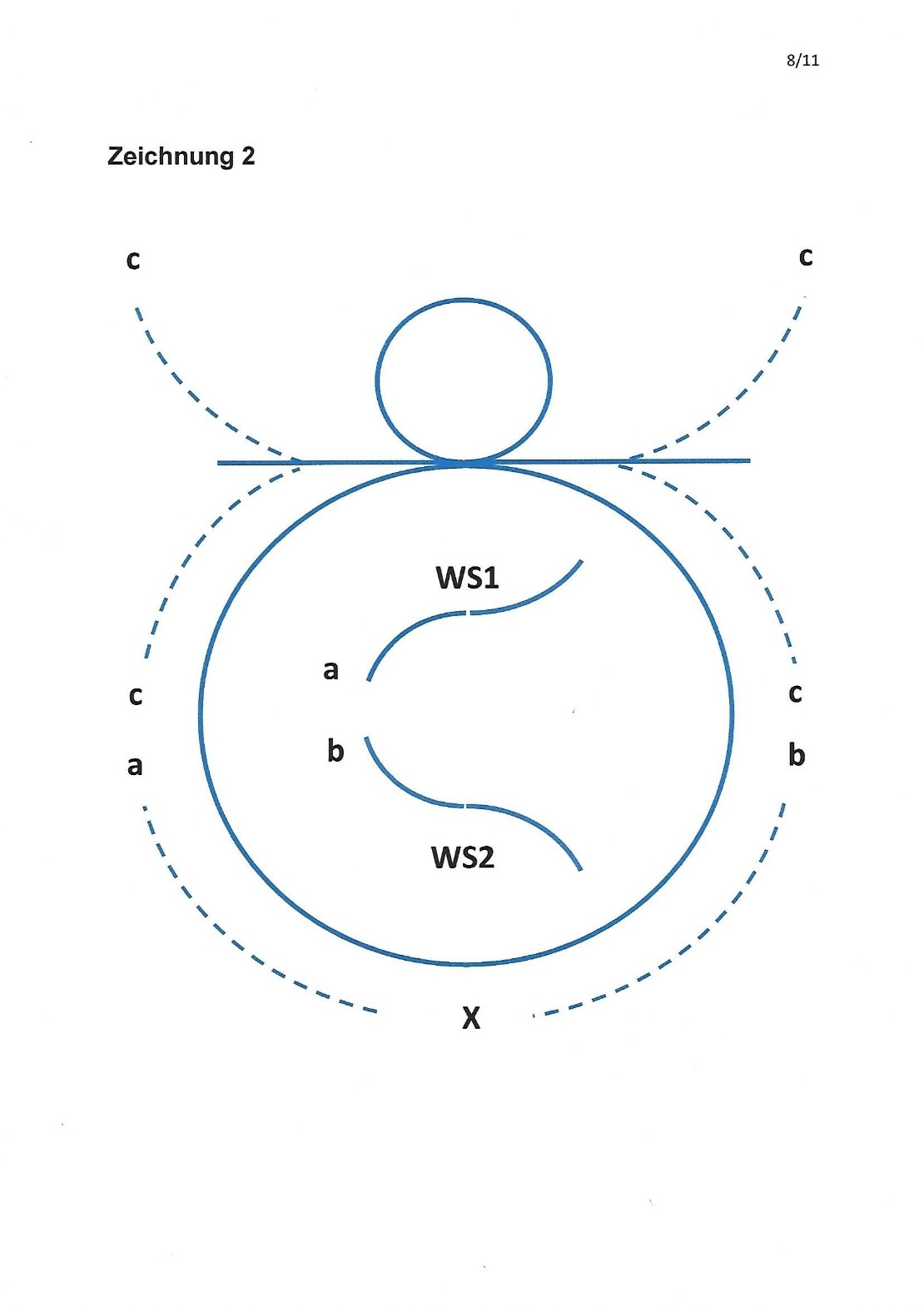
Sobald sich die Kreise zur Achter-Form zusammenschliessen entstehen die erwähnten Singularitäten, ein Doppel-Punkt und mit ihm eine Doppel-Tangente (siehe auch Zeichnung 2).
Diese Achter-Form kann auf drei verschiedene Arten durchlaufen werden:
1. Durchlauf der Achter-Kurve vom Punkt X aus im Durchlaufsinn a
Die Achter-Kurve kann ich, vom Punkt X aus zunächst nach links beginnend, durchlaufen (Durchlaufsinn a in Zeichnung 2). Ich bewege ich mich also auf einem Kurvenbogen, der sich, von „oben“ gesehen, also von einem Punkt senkrecht über dem Mittelpunkt des grossen Kreises betrachtet, im Uhrzeigersinn krümmt.
Im Doppel-Punkt ändert sich der Drehsinn der Krümmung. Ich bewege mich auf der im Gegenuhrzeigersinn gekrümmten Kurve des Achter-Kopfes wieder bis zum Doppel-Punkt, ändere dort den Drehsinn erneut und gelange auf dem im Uhrzeigersinn gekrümmten Bogen wieder nach X zurück.
2. Durchlauf der Achter-Kurve vom Punkt X aus im Durchlaufsinn b
Die Kurve kann ich von X aus auch nach rechts beginnend durchlaufen (Durchlaufsinn b). Dabei geht es zuerst im Gegenuhrzeigersinn drehend durch den Kurvenbogen zum Doppel-Punkt, dann im Uhrzeigersinn drehend durch den Kopf der Achter-Form zum Doppel-Punkt zurück und wieder im Gegenuhrzeigersinn drehend nach X zurück.
Offensichtlich ist der Doppel-Punkt also auch eine Wende-Stelle und die Doppel-Tangente ist die zugehörige Wende-Tangente.
Die beiden gegenläufigen Durchlaufrichtungen a und b sind zwar gleichwertig, die durchlaufenen Kurvenstücke um den Doppel-Punkt herum sind jedoch nicht identisch.
Im Bauch der Achter-Form habe ich je ein Stück der Kurve um die Wende-Stelle herum mit Durchlaufsinn a beziehungsweise b gezeichnet (Zeichnung 2, Mitte).
Die beiden Kurvenstücke a und b lassen sich durch Drehen in der Ebene nicht zur Deckung bringen. Dies hat mich dazu veranlasst, eine Wende-Stelle WS1 und eine Wende-Stelle WS2 zu unterscheiden. WS1 und WS2 fallen mit dem Doppel-Punkt zusammen, Daher ist der Doppel-Punkt gleichzeitig auch eine Doppel-Wende-Stelle und die Doppel-Tangente eine Doppel-Wende-Tangente.
3. Durchlauf der Achter-Kurve im Durchlaufsinn c
Die Kurve lässt sich noch in einer weiteren Art durchlaufen: Im Doppel-Punkt kann ich die Durchlaufrichtung umkehren, es entsteht dann dort eine Dorn-Spitze. Wenn ich wieder beim Doppel-Punkt angelangt bin, wechsle ich nochmals die Richtung und es entsteht eine zweite Dorn-Spitze.
Die zu den Dorn-Spitzen gehörenden Dorn-Spitz-Tangenten fallen mit der Doppel-Tangente zusammen. Im Doppel-Punkt liegen also auch noch eine Doppel-Dorn-Spitze und eine Doppel-Dorn-Spitz-Tangente vor.
Die Singularitäten der Achter-Form habe ich nachfolgend aufgelistet und mich gefragt, wie wohl die allfällige Gegenform zur Achter-Form aussehen müsste. Zu jeder Singularität muss ja die entsprechende polare Singularität zu finden sein.
Form Gegenform
Doppel-Punkt Doppel-Tangente
Doppel-Tangente Doppel-Punkt
Doppel-Wende-Stelle Doppel-Dorn-Spitz-Tangente
Doppel-Wende-Tangente Doppel-Dorn-Spitze
Doppel-Dorn-Spitze Doppel-Wende-Tangente
Doppel-Dorn-Spitz-Tangente Doppel-Wende-Stelle
Die Auflistung zeigt, dass jede Singularität der Form in der Gegenform auch vorhanden ist. Die Achter-Kurve ist also selbstpolar, der Aspekt von Form und Gegenform ist derselbe.
Ich fand es zunächst ungewöhnlich, dass der Doppel-Punkt gleichzeitig als Doppel-Wende-Stelle und als Doppel-Dorn-Spitze bezeichnet wird. Die Doppel-Tangente ist auch noch eine Doppel-Wende-Tangente mit einer Doppel-Wende-Stelle und sogar noch eine Doppel-Dorn-Spitze mit Doppel-Dorn-Spitz-Tangente. Gewöhnlich genügt zur Charakterisierung einer Singularität eine einzige Bezeichnung, aber im vorliegenden Fall scheinen mir Mehrfach-Funktionen und -Bezeichnungen einer Singularität unvermeidlich.
Übergang von der Achter-Form zur Dellen-Form
Beim Übergang von der Achter-Form zur Dellen-Form ändern sich die Singularitäten sprunghaft. Die aufgelisteten Singularitäten der Achter-Form verschwinden, sobald eine infinitesimal kleine Delle im plastisch verformbaren Ring entsteht und mit einem Schlag entstehen die Singularitäten der Dellen-Form, die Doppel-Tangente und die beiden Wendetangenten. Diese Metamorphose ist leicht nachvollziehbar.
Übergang von der Achter-Form zur rot gezeichneten Gegenform der Dellen-Form?
Wie komme ich nun aber von der rechts in Zeichnung 1 gezeichneten roten Achter-Form zur Gegenform der Dellen-Form, die als Singularitäten einen Doppel-Punkt, zwei Dorn-Spitzen und zwei Dorn-Spitz-Tangenten aufweisen muss? Ich nenne diese Gegenform die „Dorn-Spitzen/Doppel-Punkt-Form“. Wie kann ich mir da einen kontinuierlichen Übergang vorstellen? Es sollte doch, wie bei der „Dellen-Form“, eine Möglichkeit geben, die „Dorn-Spitzen/Doppel-Punkt-Form“ ebenso kontinuierlich aus dem grossen roten Kreis heraus entstehen zu lassen.
Folgendes habe ich mir dazu überlegt: Den Kopf der Achter-Form lasse ich zu einem Punkt schrumpfen und das heisst, dieser Punkt fällt mit dem Doppel-Punkt zusammen. Dieser wird zu einem gewöhnlichen Kurvenpunkt, die Mehrfachfunktionen der Singularitäten der Achter-Form entfallen, es ist nur noch ein einziger Kreis vorhanden, in Zeichnung 3 oben schwarz gezeichnet. Dieser soll - im Gegensatz zum grossen blauen Ring in Zeichnung 1 – ein elastisch verformbarer Ring sein. Das heisst, wenn der rote Ring verformt wird und die verformende Kraft zu wirken aufhört, dann federt der Ring wieder in seine ursprüngliche Kreisform zurück.
Jetzt drücke ich mit einer Nadelspitze eine Ecke in den Ring, siehe Zeichnung 3 oben. Dabei entsteht eine Reguläre Ecke, wie in FGEK Seite 96 Figur 96 dargestellt. Zu der Ecke gehören die zwei Tangenten a und b.
Anschliessend ziehe ich das Ende des einen Eckenastes auf der Tangente a, den anderen auf Tangente b nach aussen. Die Bogen, die die Reguläre Ecke gebildet haben, sollen dabei ihre Krümmung beibehalten. Das bedeutet, der Schnittpunkt der Ecktangenten entfernt sich dabei von der Kurve und es entsteht wieder ein Doppel-Punkt (Zeichnung 3 unten links). Anschliessend verbinde ich die freien Bogenenden mit einem Einfachen Bogen, so dass die zwei erforderlichen Dorn-Spitzen entstehen (Zeichnung 3 unten rechts).
Bei diesem Vorgang bleibt die Reguläre Ecke natürlich bestehen, aber ausserdem sind jetzt eine Dorn-Ecke (wie in FGEK Seite 97, Figur 97 gezeichnet) und zwei Wende-Ecken (wie in FGEK Seite 97, Figur 98 gezeichnet) entstanden. Da bei den Wende-Ecken die Eck-Punkte sowie die Eck-Tangenten zusammenfallen, bezeichne ich diese Singularität als Doppel-Wende-Ecke.
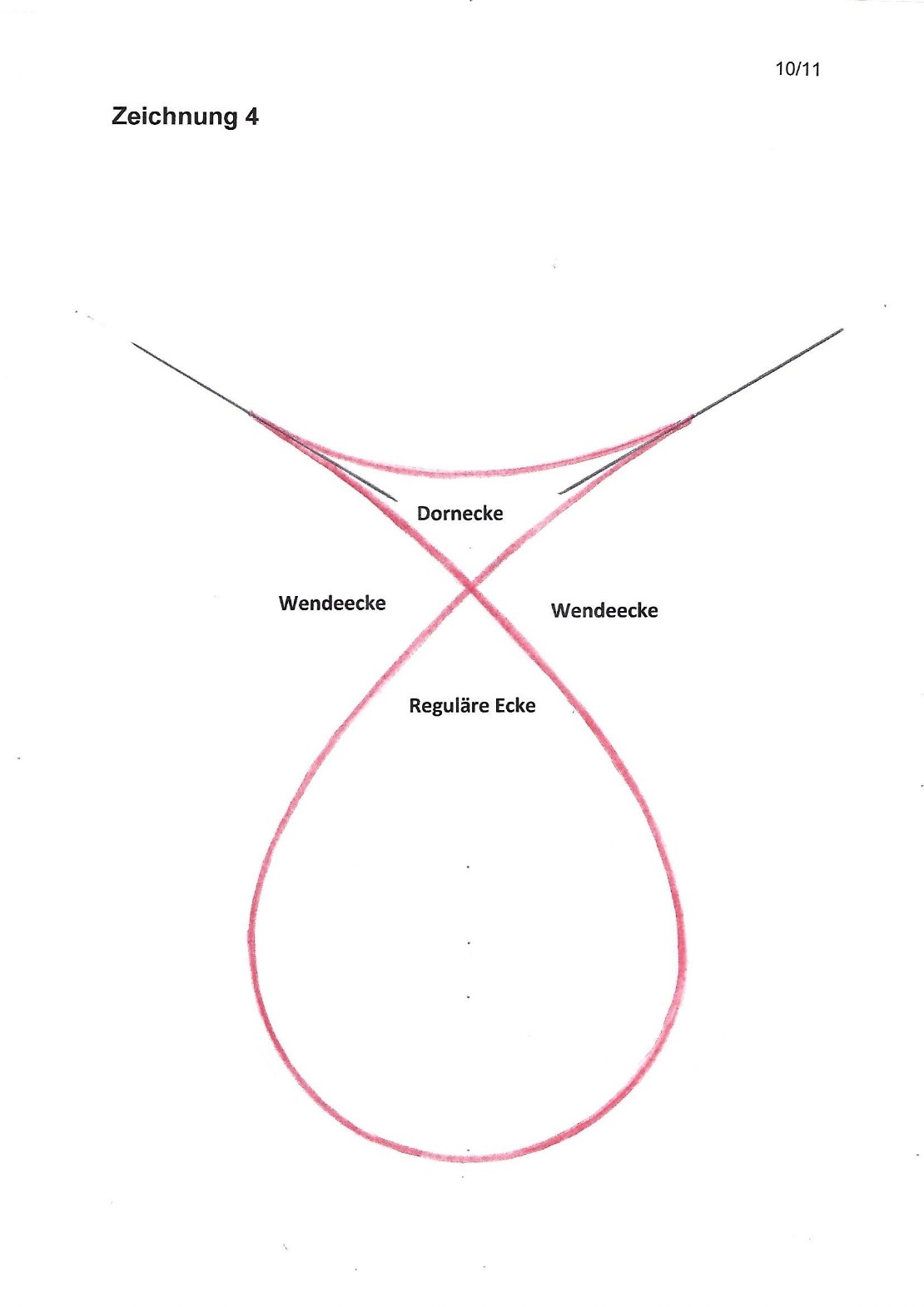
Auf diese Weise kann ich mir vorstellen, wie aus dem elastisch verformbaren, kreisförmigen Ring in kleinen und kleinsten Schritten die Dorn-Spitzen/Doppel-Punkt-Form entstehen kann. Sie ist in Zeichnung 4 mit den zugehörigen Ecken nochmals dargestellt.
Vergleich der Singularitäten der Dellen-Form mit denjenigen der Dorn-Spitzen/Doppel-Punkt-Form
In der Dorn-Spitzen/Doppel-Punkt-Form in Zeichnung 4 sind nun neben den bereits erwähnten Singularitäten, den Dorn-Spitzen und dem Doppel-Punkt noch eine Reguläre Ecke, eine Dorn-Ecke und eine Doppel-Wendeecke vorhanden.
In der Dellen-Form müssten also noch die polaren Singularitäten, nämlich eine Reguläre Strecke, eine Wendestrecke und zwei Spitzenstrecken vorhanden sein.
Wo sind diese Strecken zu finden? Es kann ja nicht sein, dass die Dellen-Form drei Singularitäten weniger aufweist als die Gegenform, nicht wahr?
Einen Ausweg aus dieser Asymmetrie sehe ich in folgendem:
Die Doppel-Tangente als integraler Teil der Dellen-Form
Ich betrachte die Doppel-Tangente (dt) in der Dellen-Form als integralen Teil der Kurve, so wie ja auch der Doppel-Punkt in der Dorn-Spitzen/Doppel-Punkt-Form integraler Teil der Kurve ist.
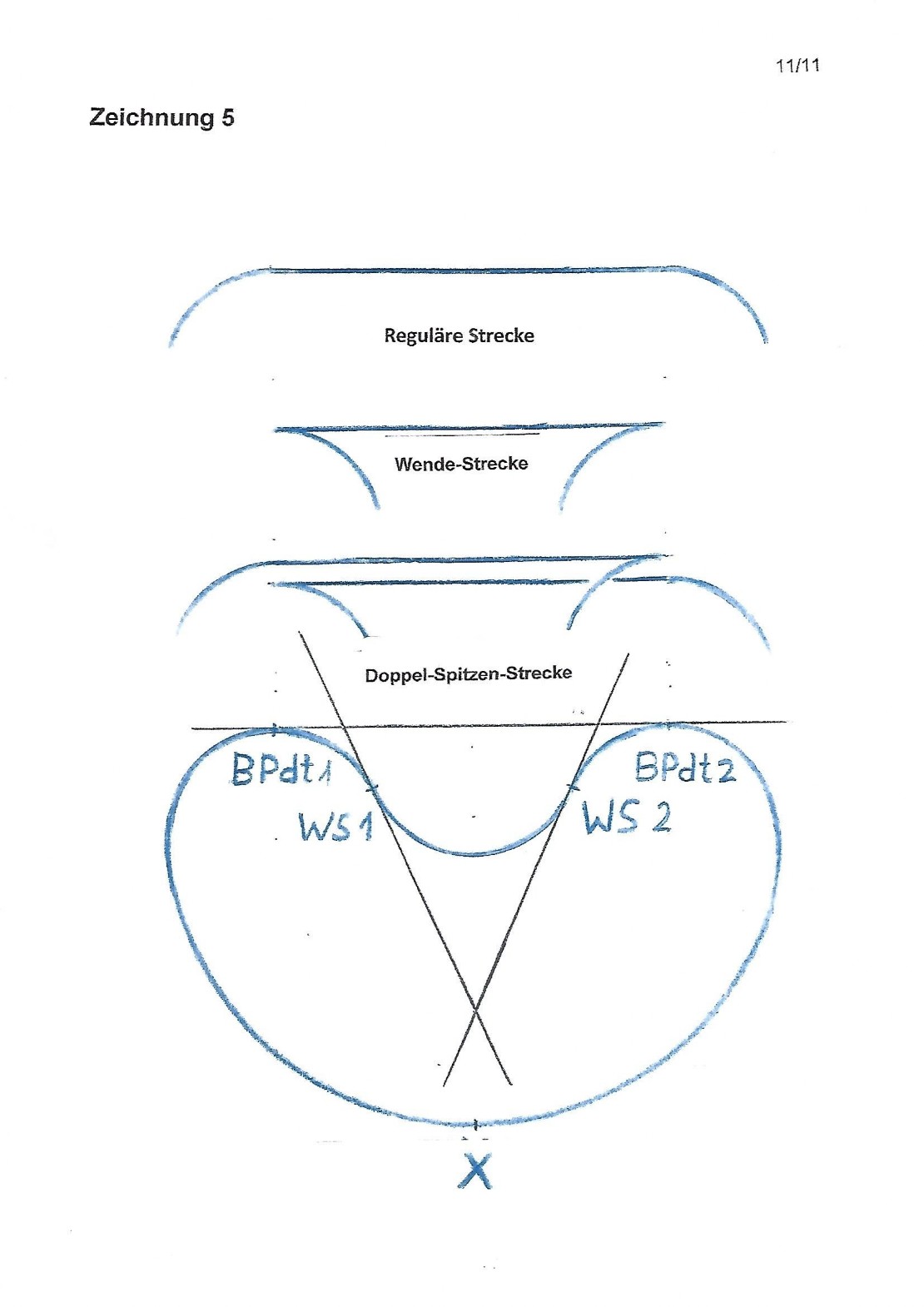
Unter dieser Voraussetzung können Teile der Kurve auf mehrere Arten durchlaufen werden. Der Ausgangspunkt X der Durchläufe ist in Zeichnung 5 eingezeichnet.
1. Vom Ausgangspunkt X geht es auf dem Einfachen Bogen zum Berührungspunkt 1 der Doppel-Tangente (BPdt1) und weiter zur ersten Wende-Stelle (WS1), dann zur zweiten Wende-Stelle (WS2) und über den Einfachen Bogen zurück zum Ausgangspunkt. Das ist der gewohnte, quasi „natürliche“ Durchlauf der ganzen Dellen-Form.
2. Zum Durchlauf 1 gibt es natürlich auch den gegenläufigen Durchlaufsinn von X zuerst zu WS2, dann zu WS1 und zurück zu X. Dies sei nur der Vollständigkeit halber erwähnt.
3. Von X auf dem Einfachen Bogen zu BPdt1, dann auf der Doppel-Tangente zu BPdt2 und über den Einfachen Bogen zurück zu X. Dieser Teil der Kurve enthält eine Reguläre Strecke, wie sie in FGEK Seite 96, Figur 104 oben gezeichnet ist.
4. Von WS1 nach BPdt1, dort Richtungswechsel und auf der Doppel-Tangente nach BPdt2, dort erneuter Richtungswechsel und weiter zu WS2 Dieser Teil der Kurve enthält eine Wende-Strecke wie in FGEK Seite 97 Figur 105 unten gezeichnet.
5. Von X zu BPdt1, auf der Doppeltangente weiter zu BPdt2, dort Richtungswechsel, zu WS2. Dieser Teil der Kurve enthält eine Spitzen-Strecke wie in FGEK Seite 97 Figur 106 unten gezeichnet.
6. Von X im umgekehrten Durchlaufsinn als vorher zu BPdt2, auf der Doppel-Tangente weiter zu BPdt1, dort Richtungswechsel, zu WS1. Dieser Teil der Kurve enthält die zweite Spitzen-Strecke, die spiegelbildlich zu derjenigen in 5. ist.
In den beiden Spitzen-Strecken wird ein Stück der Doppel-Tangente zweimal durchlaufen. Zunächst habe ich mich ein wenig an diesem Befund gestört. Aber wie sich in Zeichnung 2 die Kurverstücke mit den Wende-Stellen beim Drehen in der Ebene nicht zur Deckung bringen lassen und daher doppelt gezählt werden, ist dies auch bei den Spitzenstecken angebracht, so dass es sich um eine Doppel-Spitzen-Strecke handelt.
Die vollständige Singularitätenliste für Figur FGEK 60a sieht dann so aus.:
Dellen-Form Dorn-Spitzen/Doppel-Punkt-Form
1 Doppel-Tangente 1 Doppel-Punkt
2 Wende-Tangenten 2 Dorn-Spitzen
2 Wende-Stellen 2 Dorn-Spitz-Tangenten
1 Reguläre Strecke 1 Reguläre Ecke
1 Wende-Strecke 1 Dorn-Ecke
1 Doppel-Spitzen-Strecke 1 Doppel-Wende-Ecke
Zusammenfassung
Es scheint also möglich zu sein, Form und Gegenform in FGEK Figur 60a aus einem Kreis ohne Sprünge im Aspekt der Formen zu entwickeln.
Bei den Singularitäten ergeben sich allerdings unvermeidbare Sprünge, etwa bei der Entstehung der Achter-Form und dann bei der Aufspaltung der selbstpolaren Achter-Form in die Form und ihre polare Gegenform, also in die Dellen- und die Dorn-Spitzen/Doppel-Punkt-Form.
Singularitäten als Konstanten in einer Vielfalt von zugehörigen Formen
Die erwähnte sprunghafte Veränderung der Singularitäten ist erstaunlich, wenn ich bedenke, dass bei gegebenen Singularitäten der Aspekt der zugehörigen Kurven eine unendliche Vielfalt an Formen zulässt. Ich habe in den Zeichnungen nur spiegelsymmetrische Formen gezeichnet. Die Spiegelsymmetrie ist jedoch keineswegs wesentlich, der Aspekt der Kurven kann völlig «verzerrt» erscheinen, die Singularitäten bleiben in allen Form-Varianten dieselben.
Zudem können die verwendeten Kreise genauso gut Ei-Linien sein, letztere weisen ja auch keine Singularitäten auf.
Kontinuierliche Verwandlung des Kurven-Aspekts, aber sprunghafte Änderungen der zugehörigen Singularitäten
Die Verwandlung des Aspekts einer Kurve, etwa des Kreises in die Dellen-Form, erscheint mir als ein kontinuierlicher Ablauf, während die Singularitäten sich während dieses Vorgangs sprunghaft ändern.
Verwandlung «Kreis in Dellen-Form»: einfach nachvollziehbar
Die Verwandlung von Kreis/Ei-Linie in die Achter-Form und dann in die Dellen-Form ist einfach nachvollziehbar. Der starr gedachte kleine Kreis drückt eine Delle in den plastisch verformbaren Ring.
Verwandlung «Kreis in Dorn-Spitzen/Doppel-Punkt-Form»: komplex
Die Metamorphose von der Achter-Form in die Dorn-Spitzen/Doppel-Punkt-Form ist schwieriger. Es sind mehrere Schritte erforderlich, zuerst muss – jedenfalls gemäss meinem Vorgehen - eine Reguläre Ecke entstehen, Die Bogen müssen über den Eckpunkt hinaus verlängert werden, damit der Doppel-Punkt entsteht und gleichzeitig muss ein zusätzlicher Einfacher Bogen herangezogen werden, um die Dorn-Spitzen entstehen zu lassen.
Bei diesem Vorgang sind zusätzliche Singularitäten (Reguläre Ecke, Dorn-Ecke und Doppel-Wende--Ecke) entstanden. Zu diesen waren in der Dellen-Form die dazu polaren Strecken zu finden.
Ausblick
Die Metamorphosen können natürlich in verschiedener Weise weitergeführt werden. Naheliegend ist, die Bewegung in Zeichnung 1 gradlinig weiterzuführen. Dann ergibt sich eine ausgezeichnete Lage, wenn der Schnittpunkt der beiden Wende-Tangenten der Dellen-Form auf die Kurve zu liegen kommt (FGEK, Figur 60b). Dies hat auf den Aspekt der Dellen-Form keinen Einfluss, wohl aber auf den Aspekt der Gegenform, der Dorn-Spitzen/Doppel-Punkt-Form. Mehr dazu in einem weiteren Kapitel.